About 7,000 species of fishes are used by humans for food, sports, the aquarium trade, or are threatened by environmental degradation. However, life history parameters such as growth and size at first maturity, which are important for management, are known for less than 2,000 species. We therefore created a life history ‘Key Facts’ page that strives to provide estimates with error margins of important life-history parameters for all fishes (select a species and click on the Key facts link). It uses the ‘best’ available data in FishBase as defaults for various equations, as explained below. Users can replace these defaults with their own estimates and recalculate the parameters. For most parameters, we present the range of the standard error of the estimate, which contains about 2/3 of the range of the observed values. We will gradually replace these with estimates of the 95% confidence limits, derived from the standardized residuals. We hope the Key Facts will prove useful to managers and conservationists in species-rich and data-poor tropical countries.
Life history parameters
Max. length: The maximum size of an organism is a strong predictor for many life history parameters (e.g., Blueweiss et al. 1978). The default value used here is the maximum length (Lmax) ever reported for the species in question, which is in principle available for all species of fish. If no other data are available, this value is used to estimate asymptotic length (Linf), length at first maturity (Lm), and length of maximum possible yield (Lopt), as defined in more detail below. However, Lmax may be much higher than the maximum length reached by the fish population being studied by the user, in which case the derived estimates will be unrealistically high. If additional maximum size estimates for different areas are available in FishBase, a click on the Max. size data link displays a list that can be used to replace the Lmax value with more appropriate estimates. If the Recalculate button in the Max. length row is clicked, Linf , Lm and Lopt are recalculated.
L infinity: This is the length (Linf) that the fish of a population would reach if they were to grow indefinitely (also known as asymptotic length). It is one of the three parameters of the von Bertalanffy growth function: Lt = Linf (1 – e –K(t-to)); where Lt is the length at age t (see below for definitions of K and t0). If one or more growth studies are available in FishBase, Linf of the population with the median Ø’ (see definition below) is taken. Users can click on ‘Growth data’ to see a list of the different estimates of Linf for different populations, i.e. from different localities, of the species in question. If no growth studies are available, Linf and the corresponding 95% confidence interval are estimated from maximum length using an empirical relationship between Linf and Lmax (Froese and Binohlan 2000). Users can change the Linf value and click the Recalculate button to update all parameters depending on Linf.
K:
t0: This is another parameter of the von Bertalanffy growth function which is defined as the hypothetical age (in years) the fish would have had at zero length, had their early life stages grown in the manner described by the growth equation¾
which in most fishes is not the case. Its effect is to move the whole growth curve sideways along the X-axis without affecting either Linf or K. Many growth studies use methods that do not provide realistic estimates of t0 and thus result in ‘relative’ age at length. To improve the estimation of life span and generation time below, we use an empirical equation (Pauly 1979) to estimate a default value for t0 from Linf and K. This has the form: log (-t0) = -0.3922 - 0.2752 log Linf - 1.038 log K. Users can replace the default value and recalculate life span and age at first maturity.
Natural mortality: The instantaneous rate of natural mortality (M; 1/year) refers to the late juvenile and adult phases of a population and is calculated here from Pauly’s (1980) empirical equation based on the parameters of the von Bertalanffy growth function and on the mean annual water temperature (T), using a re-estimated version that analyzes a larger dataset and provides confidence limits. The Growth data link shows other estimates of M and water temperature. Users can change the values for Linf, K and annual water temperature and recalculate the value of M. If no estimate of K is available, M is calculated from the preliminary empirical equation: M = 10^(0.566 - 0.718 * log(Linf) + 0.02 * T (Froese et al. in prep.). Note that the length type for calculating M has to be fork length for scombroids (tuna and tuna-like fishes) and total length for all other fishes. Length is used here mainly as a ‘proxy’ for weight. Thus, natural mortality will be underestimated in eel-like fishes and overestimated in sphere-shaped fishes.
Life span: This is the approximate maximum age (tmax) that fish of a given population would reach. Following Taylor (1958), it is calculated as the age at 95% of Linf, using the parameters of the von Bertalanffy growth function as estimated above, viz.: tmax = t0 + 3 / K.
L maturity:
Age at first maturity:
L max. yield: This is the length class (Lopt) with the highest biomass in an unfished population, where the number of survivors multiplied with their average weight reaches a maximum (Beverton 1992). A fishery would obtain the maximum possible yield if it were to catch only fish of this size. Thus, fisheries managers should strive to adjust the mean length in their catch towards this value. They can also use Lm and Lopt to evaluate length-frequency diagrams for signs of growth overfishing (capturing fish before they have realized most of their growth potential) and recruitment overfishing (reducing the number of parents to a level that is insufficient to maintain the stock and hence the fishery; see Fig. 33). If no growth parameters are available, Lopt and its standard error are estimated from an empirical relationship between Lopt and Linf (Froese and Binohlan 2000). Otherwise, Lopt is estimated from the parameters of the von Bertalanffy growth function and natural mortality as: Lopt = Linf * (3 / (3 + M/K)) (Beverton 1992).
Relative yield-per-recruit:
Exploitation rate:
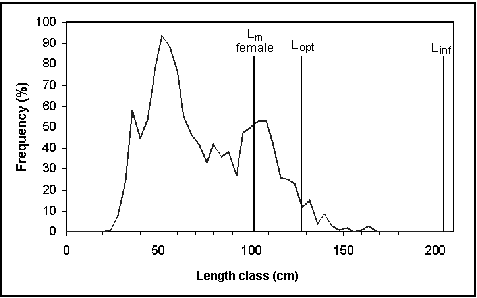
Fig. 33. Length-frequency data of commercial Nile perch catches in Lake Victoria (Asila and Ogari 1988) plotted in a simple framework indicating L¥
, Lm and Lopt. Note that the length distribution indicates growth and recruitment overfishing. The yield could be increased by a factor of about 2.4 if all fishes smaller than Lopt were caught at a length between Lm and Lopt.
Estimation of exploitation rate from mean length in catches: Beverton and Holt (1956) showed that for fish that grow according to the von Bertalanffy growth function, total mortality (Z) can be expressed by: Z = K * (Linf – Lmean) / (Lmean – L’) , where Lmean is the mean length of all fishes caught at sizes equal or larger than L’, which is the smallest size in the catch and here assumed to be the same as Lc, which is the mean length at entry in the fishery, assuming knife-edge selection, and thus the same as used under Yield per Recruit above. All other parameters are as defined above. Users can enter observed values of Lc and Lmean for a given fishery, as may be estimated from length-frequency samples, and calculate total mortality Z, fishing mortality F = Z – M, and exploitation rate E = F / Z. The estimate of F or E can then be compared with those at maximum sustainable yield and optimum yield as given in the Relative Yield per Recruit section, thus obtaining a preliminary indication of the status of the fishery. Note, however, that the length-frequencies from which L
c and Lmean are derived must be to the furthest extent possible representative of the length-structure of the population under equilibrium, as may be obtained by averaging a long time series of length-frequency samples.
Resilience / productivity: The American Fisheries Society (AFS) has suggested values for several biological parameters that allow to classify a fish population or species into categories of high, medium, low and very low resilience or productivity (Musick 1999; Tab. 1). If no reliable estimate of rm (see below) is available, the assignment is to the lowest category for which any of the available parameters fits. For each of these categories, AFS has suggested thresholds for decline over the longer of 10 years or three generations. If an observed decline measured in biomass or numbers of mature individuals exceeds the indicated threshold value, the population or species is considered vulnerable to extinction unless explicitly shown otherwise. If one sex strongly limits the reproductive capacity of the species or population, then only the decline in the limiting sex should be considered. We decided to restrict the automatic assignment of resilience categories in the Key Facts page to values of K, tm and tmax and those records of fecundity estimates that referred to minimum number of eggs or pups per female per year, assuming that these were equivalent to average fecundity at first maturity (Musick 1999). Note that many small fishes may spawn several times per year (we exclude these for the time being) and large live bearers such as the coelacanth may have gestation periods of more than one year (we corrected fecundity estimates for those cases reported in the literature). Also, we excluded resilience estimates based on rm (see below) as we are not yet confident with the reliability of the current method for estimating rm. If users have independent rm or fecundity estimates, they can refer to Table 1 for using this information.
|
Parameter |
High |
Medium |
Low |
Very low |
|
Threshold |
0.99 |
0.95 |
0.85 |
0.70 |
|
rmax (1/year) |
> 0.5 |
0.16 – 0.50 |
0.05 – 0.15 |
< 0.05 |
|
K (1/year) |
> 0.3 |
0.16 – 0.30 |
0.05 – 0.15 |
< 0.05 |
|
Fecundity (1/year) |
> 10,000 |
100 – 1000 |
10 – 100 |
< 10 |
|
tm (years) |
< 1 |
2 – 4 |
5 – 10 |
> 10 |
|
tmax (years) |
1 – 3 |
4 – 10 |
11 – 30 |
> 30 |
| rmis difficult to estimate in fishes |
Intrinsic rate of population increase: The intrinsic rate of population growth (rm; 1/year) has been suggested as a useful parameter to estimate the capacity of species to withstand exploitation (see above). It also largely simplifies the parametrization of Schaefer models for estimating maximum sustainable yield through the relationship MSY = rm * Binf / 4, where Binf is the maximum biomass of a particular species that a given ecosystem can support (Ricker 1975), often corresponding to the original size of the unfished population. Note that if Lc is close to the average length Lr at which juveniles join the parent stock, then the value of FMSY (above) can be used to estimate rm from the relationship rm = 2 * FMSY (Ricker 1975). It seems that 0.4 * Linf is a first approximation of Lr. We are exploring this and other options to estimate rm. One can calculate the time (td) in years that it would take a strongly reduced population to double in numbers if all fishing ends, from td = ln(2) / rm.
|
|
| Our approach to estimate generation time |
Generation time: This is the average age (tg) of parents at the time their young are born. In most fishes Lopt (see above) is the size class with the maximum egg production (Beverton 1992). The corresponding age (topt) is a good approximation of generation time in fishes. It is calculated using the parameters of the von Bertalanffy growth function as tg = topt = t0 - ln(1 - Lopt / Linf) / K. Note that in small fishes (< 10 cm) maturity is often reached at a size larger than Lopt and closer to Linf. In these cases, the length class where about 100% (instead of 50%) first reach maturity will contain the highest biomass of spawning fishes, resulting usually in the highest egg production. As an approximation for that length class we assume that most fish will have reached maturity at a length that is slightly longer than Lm, viz.: Lm100 = Lm + (Linf - Lm) / 4, and calculate generation time as the age at Lm100. This is applied whenever Lm >= Lopt.
Length-weight: This equation can be used to estimate the corresponding wet weight to any given length. The default entry is Linf, thus calculating the asymptotic weight for the fish of the population in question. The parameters ‘a’ and ‘b’ are taken from data in FishBase with a median value of ‘a’ and with the same length type (TL, SL, FL) as Linf. Users can click on the ‘Length-weight’ link to see additional data. Users can change the length or the values of ‘a’ and ‘b’ and recalculate the corresponding weight.
Whole-body nitrogen and crude protein: L.J. Ramseyer (2000, in review;
see also www.mi.nmfs.gov/Nfish.html) has analysed the relationship
between whole-fish wet weight and whole-body nitrogen content for 68
species and hybrids, based on data extracted from the literature. He
found the following relationship: log N (g) = 1.03 * (log wet weight) -
1.65; n=2811, r^2=0.996, p<0.001. For the conversion from nitrogen to
crude protein he gives the ratio: crude protein = 6.25 * nitrogen. We
have added these relationships here for your convenience.
Trophic level: The rank of a species in a food web can be described by its trophic level (troph), which can be estimated as: Troph = 1 + mean trophs of food items; where the mean troph is weighted by the contribution of the various food items (Pauly and Christensen 1998). The default value and its standard error as shown in the Key Facts sheet are derived from the first of the following options that provides an estimate of troph based on: 1) diet information in FishBase, 2) food items in FishBase, and 3) size-adjusted troph estimates from species with relatives for which (1) or (2) are available (see Box 23 where the comparative method for estimating troph is described)].
|
|
| A simple tool to estimate population food consumption |
Food consumption: The amount of food ingested (Q) by an age-structured fish population expressed as a fraction of its biomass (B) is here presented by the parameter Q/B. FishBase contains over 160 independent estimates of Q/B extracted mainly from Palomares (1991) and Palomares and Pauly (1989) and also from Pauly (1989). These estimates were obtained using Pauly’s (1986) equation, viz.: Q/B = [(dW/dt) / K1(t)] / [WtNtdt] integrated between the age at which fish recruit (tr) and the maximum age of the population (tmax); where Nt is the number of fishes at age t, Wt their mean individual weight, and K1(t) their gross food conversion efficiency (= growth increment / food ingested). These Q/B estimates are available in FishBase for only 98 species and for most of these, there is only one Q/B estimate per species. In the few species for which several Q/B values are available, the median Q/B value is taken and a ‘Food consumption’ link is provided to the user for viewing the details of these studies. For other species, Q/B is estimated from the empirical relationship proposed by Palomares and Pauly (1999), viz.: log Q/B = 7.964 – 0.204 log Winf – 1.965T’ + 0.083A + 0.532h + 0.398d; where Winf (or asymptotic weight) is the mean weight that a population would reach if it were to grow indefinitely, T’ is the mean environmental temperature expressed as 1000 / (C + 273.15), A is the aspect ratio of the caudal fin indicative of metabolic activity and expressed as the ratio of the square of the height of the caudal fin and its surface area, ‘h’ and ‘d’ are dummy variables indicating herbivores (h=1, d=0), detritivores (h=0, d=1) and carnivores (h=0, d=0). The default value for Winf is taken either from Linf and the length-weight relationship (see above) or from Wmax (maximum weight ever recorded for the species) when an independent estimate of Winf is not available in FishBase. Values of A were assigned, for each of the different shapes of caudal fins considered here, using the median A values based on 125 records in FishBase of species with A and caudal fin shape data (from left to right: lunate, forked, emarginate, truncate, round, pointed, double emarginate and heterocercal). Note that five of these eight shapes share the same median value, that which is used as the default A value for the empirical estimation of Q/B when an independent estimate is not available. We are working on a method that will better separate categories of caudal fins. Values of the feeding type indicators ‘d’ and ‘h’ are assigned according to which feeding category the species belongs: detritivore, herbivore, omnivore (default) and carnivore. These categories are determined either from the Main food or the Trophic level (detritivores troph < 2.2; herbivores troph < 2.8; carnivores troph > 2.8). When the default category ‘Omnivore’ is highlighted, Q/B is estimated as the mean of the Q/B values obtained for herbivores and carnivores. The temperature used in the estimation of M above is applied in the empirical estimation of Q/B. The Q/B estimate is automatically recalculated when the tail fin shape and/or the feeding types are changed. The Recalculate button is provided when values of Winf and A are re-entered, e.g., in cases where no possible/guessed values of Winf are available in FishBase.
|
|
| Comments |
The Key Facts page is still very much evolving and we welcome comments and suggestions for its further improvement to any of the authors.
|
|
| Acknowledgments |
We thank Eli Agbayani for programming the many changes we requested when developing the Key Facts page. We thank the FishBase Team for assembling the data that allowed us to implement this approach.
|
|
| How to get there |
You get to the KEY FACTS routine by clicking on the respective button in the BIOLOGY window of the species in question.
|
|
| Internet |
On the Internet, you get to the ‘Key Facts’ page by clicking the respective link in the ‘More information’ section of the ‘Species Summary’ page. Note that you can save the Key Facts page to your harddisk and that it will function off-line.
|
|
| References |
Asila, A.A. and J. Ogari. 1988. Growth parameters and mortality rates of Nile perch (Lates niloticus) estimated from length-frequency data in the Nyanza Gulf (Lake Victoria), p. 272-287. In S. Venema, J. Möller-Christensen and D. Pauly (eds.) Contributions to tropical fisheries biology: papers by the participants of the FAO/DANIDA follow-up training courses. FAO Fish. Rep., (389): 519 p.
Beddington, J.R. and J.G. Cooke. 1983. The potential yield of fish stocks. FAO Fish. Tech. Pap. (242), 47 p.
Beverton, R.J.H. and S.J. Holt. 1956. A review of methods for estimating mortality rates in fish populations, with special references to sources of bias in catch sampling. Rapp. P.-V. Réun. CIEM 140:67-83.
Beverton, R.J.H. and S.J. Holt. 1957. On the dynamics of exploited fish populations. Fish. Invest. Ser. II. Vol. 19, 533 p.
Beverton, R.J.H. and S.J. Holt. 1964. Table of yield functions for fisheries management. FAO Fish. Tech. Pap. 38, 49 p.
Beverton, R.J.H. 1992. Patterns of reproductive strategy parameters in some marine teleost fishes. J. Fish Biol. 41(B):137-160
Blueweiss, L., H. Fox, V. Kudzman, D. Nakashima, R. Peters and S. Sams. 1978. Relationships between body size and some life history parameters. Oecologia 37:257-272
Froese, R. and C. Binohlan. 2000. Empirical relationships to estimate asymptotic length, length at first maturity and length at maximum yield per recruit in fishes, with a simple method to evaluate length frequency data. J. Fish Biol. 56:758-773.
Froese, R., C. Binohlan and D. Pauly. Empirical equations to estimate natural mortality in fishes. (In prep.).
Gulland, J.A. 1971. The fish resources of the oceans. FAO/Fishing News Books, Surrey, UK.
Musick, J.A. 1999. Criteria to define extinction risk in marine fishes. Fisheries 24(12):6-14.
Palomares, M.L.D. 1991. La consommation de nourriture chez les poissons: étude comparative, mise au point d’un modèle prédictif et application à l’étude des reseaux trophiques. Ph.D. Thesis, Institut National Polytechnique de Toulouse, France.
Palomares, M.L. and D. Pauly. 1989. A multiple regression model for predicting the food consumption of marine fish populations. Aust. J. Mar. Freshwat. Res. 40:259-273.
Palomares, M.L.D. and D. Pauly. 1999. Predicting the food consumption of fish populations as functions of mortality, food type, morphometrics, temperature and salinity. Mar. Freshwat. Res. 49:447-453.
Pauly, D. 1979. Gill size and temperature as governing factors in fish growth: a generalization of von Bertalanffy’s growth formula. Ber. Inst. f. Meereskunde Univ. Kiel. No 63, xv + 156 p.
Pauly, D. 1980. On the interrelationships between natural mortality, growth parameters, and mean environmental temperature in 175 fish stocks. J. Cons. CIEM 39(2):175-192
Pauly, D. 1984. A mechanism for the juvenile-to-adults transition in fishes. J. Cons. CIEM 41:280-284.
Pauly, D. 1986. A simple method for estimating the food consumption of fish populations from growth data and food conversion experiments. Fish. Bull. (US) 84:827-840.
Pauly, D. 1989. Food consumption by tropical and temperate fish populations: some generalizations. J. Fish Biol. 35 (Suppl. A):11-20.
Pauly, D. and V. Christensen. 1998. Trophic levels of fishes, p. 155. In R. Froese and D. Pauly (eds.) FishBase 1998: concepts, design and data sources. ICLARM, Manila, Philippines. 293 p.
Pauly, D., J. Moreau and F.C. Gayanilo, Jr. 1998. Auximetric analyses, p. 130-134. In R. Froese and D. Pauly (eds.) FishBase 1998: concepts, design and data sources. ICLARM, Manila, Philippines. 293 p.
Ricker, W.E. 1975. Computation and interpretation of biological statistics of fish populations. Bull. Fish. Res. Board Can. (191), 382 p.
Taylor, C.C. 1958. Cod growth and temperature. J. Cons. CIEM 23:366-370
|
|